Update Stress First (USF)

Update Stress First (USF)#

MPM Explicit

Update stress first refers to incrementing the stresses at the material points before calculating the internal force and consequently before solving the balance of momentum.

USF Algorithm#

at each time step $\Delta t$ from $t$ to $t + \Delta t$:

Material points carry all state variables (mass/density, velocity, strain, stress, other material parameters corresponding to the adopted constitutive relation). The state variables are initialised at every material point at the start of the time step.
Mass of each material point is computed based on its density and initial volume. The initial volume is computed based on the number of material points in cell or can be provided as an input argument. Although the density of material points are updated, the mass is conserved.

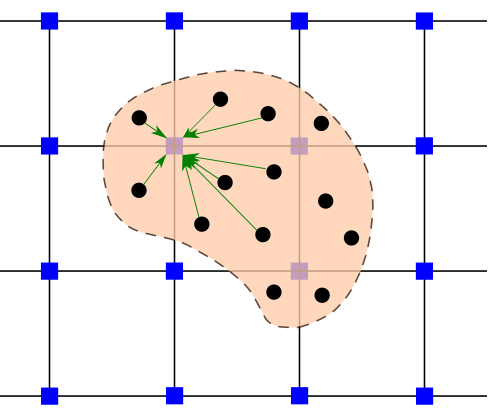
\[ m_p = \rho V_p \]
The shape functions $N_i (x_p^t)$ and the gradient of the shape functions $B_i (x_p^t)$ are computed for each material point $p$, based on the cell in which they are located.
The nodal mass and momentum are calculated based on the mass and velocity of all the material points in the cell and are mapped to the nodes using the shape functions.
- Compute nodal mass
  
  \[ m_i^t = \sum\limits_{p=1}^{n_P} N_i(\textbf{x}_p^t) m_p \]
- Compute nodal momentum
  
  \[ (m \textbf{v})_i^{t} = \sum\limits_{p=1}^{n_P} N_i(\textbf{x}_p^t) m_p \textbf{v}_p^{t} \]
The nodal velocities at each active node $i$ is computed based on the momentum and the nodal mass. An active node is defined as nodes forming a cell that contains at least one material point.

\[ \textbf{v}_i^{t} = \frac{(m\textbf{v})_i^{t}}{m_i^{t}} \]
The strain at each material point is computed by mapping the strain rate from the nodes: $$ \boldsymbol{\varepsilon}_p^t = \sum\limits_{p=1}^{n_P} B_i(\textbf{x}_p^t) \textbf{v}_i^t $$
The stress at each material point is updated using $\Delta\sigma_p^t$ based on the constitutive model: $$ \boldsymbol{\sigma}_p^t = \boldsymbol{\sigma}_p^{t-\Delta t} + \Delta \boldsymbol{\sigma}_p^t $$

\[ \Delta\boldsymbol{\sigma}_p^t= \mathbf{D} : \Delta \boldsymbol{\varepsilon}_p^t \]
Compute the nodal body force from the material points:
- Body force: $$ \textbf{b}_i^{t} = G \sum\limits_{p=1}^{n_P} N_i(\textbf{x}_p^t) m_p $$
Compute the nodal external and internal force
- External force: $$ (\textbf{f}_i)^{ext,t} = \textbf{b}_i^{t} + \textbf{t}_i^{t} $$
- Internal force: $$ (\textbf{f}_i)^{int,t} = \sum\limits_{p=1}^{n_P} V_p^t B_i(\textbf{x}_p^t) \boldsymbol{\sigma}_i^{t} $$
The nodal acceleration and velocities of the next step $ t + \Delta t$ are computed on all active nodes:
- Nodal acceleration: $$ \textbf{a}_i^{t+\Delta t} = \frac{\textbf{f}_i^{t}}{m_i^t}$$
- Nodal velocity: $$ \textbf{v}_i^{t+\Delta t} = \textbf{v}_i^{t} + \textbf{a}_i^{t+\Delta t} * \Delta t$$
Apply any velocity constraints (and acceleration constraints - when velocity is set, acceleration is set to zero) at the nodes.
Update the position of the material points based on the nodal velocity.
- Material point velocity: $$ \textbf{v}_p^{t+\Delta t} = \sum\limits_{i=1}^{n_n} N_i(\textbf{x}_p^t) \textbf{v}_i^{t+\Delta t} $$
- Material point position: $$ \textbf{x}_p^{t+\Delta t} = \textbf{x}_p^t + \textbf{v}_p^{t+\Delta t} * \Delta t$$
Locate all material points in the mesh and assign a new cell to the material point, if the material points have crossed cells.
At the end of every time step, all the variables on the grid nodes are initialised to zero. The material points carry all the information about the solution, and the computational grid is re-initialised for the next step.

Nomenclature#

General#

$G$ acceleration due to gravity ($G = 9.81 m/s^2$)

Material Point#

$\textbf{a}_p^t$ acceleration of the material point $p$ at time $t$

$m_p^t$ mass of the material point $p$ at time $t$

$m\textbf{v}_p^t$ momentum of the material point $p$ at time $t$

$n_p$ total number of material points in the body

$\textbf{t}_p^t$ traction at material point $p$

$\textbf{v}_p^t$ velocity of the material point $p$ at time $t$

$V_p$ volume at material points $p$

$\textbf{x}_p^t$ coordinates of the material point $p$ at time $t$

$\varepsilon_{v,p}^t$ volumetric strain of the material point $p$ at time $t$

$\rho$ density of the material point

Node#

$\textbf{a}_i^t$ acceleration of node $i$

$\textbf{b}_i^t$ body force of node $i$

$\textbf{f}_i^t$ nodal force of node $i$ at time $t$

$\textbf{f}_i^{ext,t}$ nodal external force of node $i$ at time $t$

$\textbf{f}_i^{int,t}$ nodal internal force of node $i$ at time $t$

$m_i^t$ mass of node $i$ at time $t$

$m\textbf{v}_i^t$ momentum of node $i$ at time $t$

$n_n$ total number of nodes in a cell

$\textbf{t}_i^t$ traction at node $i$ at time $t$

$\textbf{v}_i^t$ velocity of node $i$ at time $t$

$\boldsymbol{\varepsilon}_i^t$ strain of node $i$ at time $t$

$\boldsymbol{\sigma}_i^t$ stress of node $i$ at time $t$

Shape Functions#

$B_i (\textbf{x}_p^t)$ gradient of the shape function that maps node $i$ to material point $p$ and vice versa such that $B = \frac{dN}{d\textbf{x}}$

$N_i (\textbf{x}_p^t)$ shape function that maps node $i$ to material point $p$ and vice versa with independent variable of the location of each material point at time $t$