Material Point Method

Material Point Method (MPM) is a particle based method that represents the material as a collection of material points, and their deformations are determined by Newton’s laws of motion. The MPM is a hybrid Eulerian-Lagrangian approach, which uses moving material points and computational nodes on a background mesh. This approach is very effective particularly in the context of large deformations.

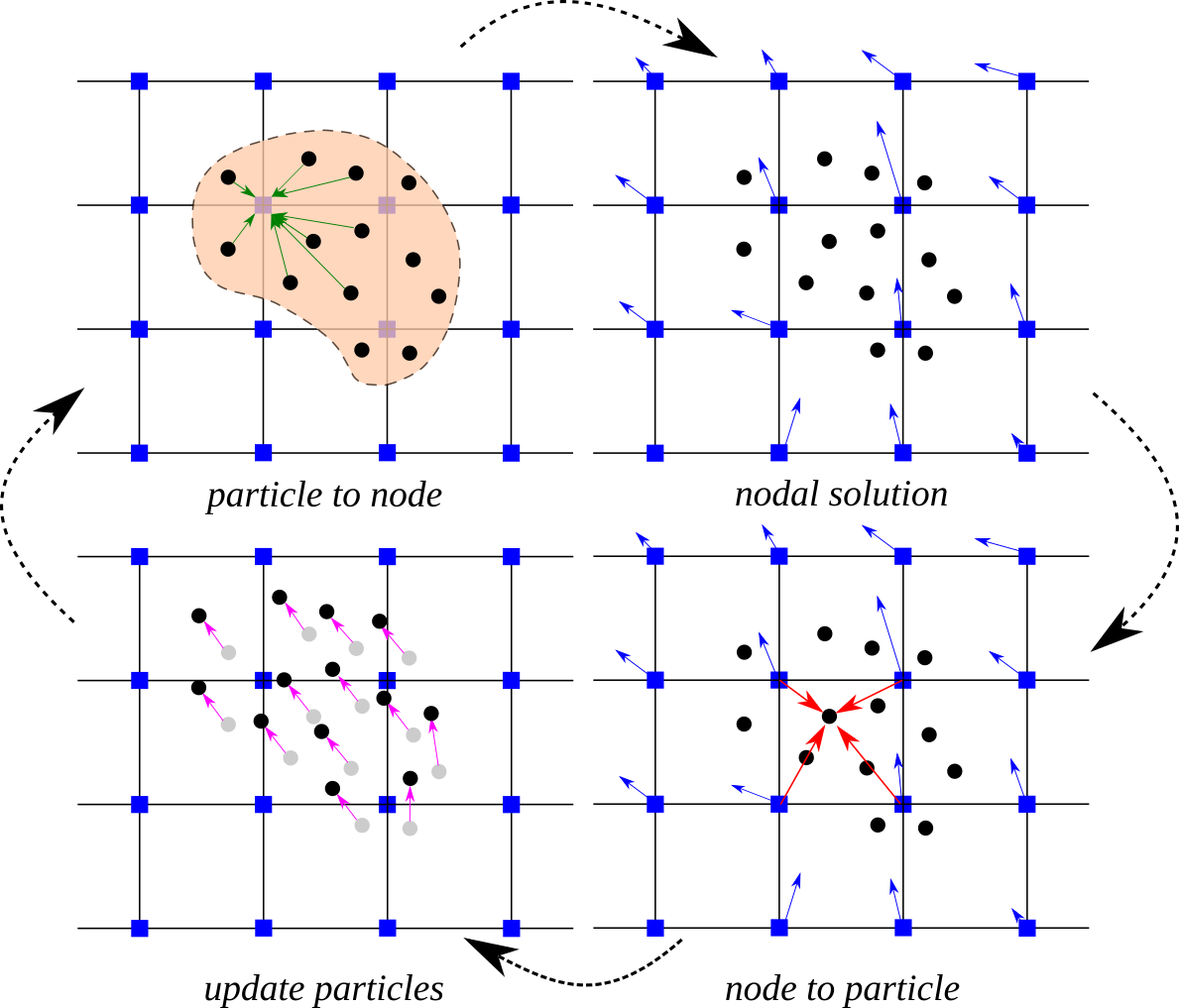
Illustration of the MPM algorithm (1) A representation of material points overlaid on a computational grid. Arrows represent material point state vectors (mass, volume, velocity, etc.) being projected to the nodes of the computational grid. (2) The equations of motion are solved onto the nodes, resulting in updated nodal velocities and positions. (3) The updated nodal kinematics are interpolated back to the material points. (4) The state of the material points is updated, and the computational grid is reset

MPM Online course book

Learn to code MPM with Python online book

CB-Geo MPM code

• The CB-Geo MPM code is available at GitHub

Documentation

• MPM documentation

Team

Publications